ALU, singkatan dari Arithmetic And Logic Unit (bahasa Indonesia: unit aritmatika dan logika), adalah salah satu bagian dalam dari sebuah mikroprosesor yang berfungsi untuk melakukan operasi hitungan aritmatika dan logika. Contoh operasi aritmatika adalah operasi penjumlahan dan pengurangan, sedangkan contoh operasi logika adalah logika AND dan OR. tugas utama dari ALU (Arithmetic And Logic Unit)adalah melakukan semua perhitungan aritmatika atau matematika yang terjadi sesuai dengan instruksi program. ALU melakukan operasi arithmatika dengan dasar pertambahan, sedang operasi arithmatika yang lainnya, seperti pengurangan, perkalian, dan pembagian dilakukan dengan dasar penjumlahan. sehingga sirkuit elektronik di ALU yang digunakan untuk melaksanakan operasi arithmatika ini disebut adder. Tugas lalin dari ALU adalah melakukan keputusan dari operasi logika sesuai dengan instruksi program. Operasi logika (logical operation) meliputi perbandingan dua buah elemen logika dengan menggunakan operator logika, yaitu:
a. sama dengan (=)
b. tidak sama dengan (<>)
c. kurang dari (<)
d. kurang atau sama dengan dari (<=)
e. lebih besar dari (>)
f. lebih besar atau sama dengan dari (>=)
 |
| Simple Expression |
Arithmatic
Logical Unit (ALU), fungsi unit ini adalah untuk melakukan suatu proses
data yang berbentuk angka dan logika, seperti data matematika dan
statistika. ALU terdiri dari register-register untuk menyimpan
informasi.Tugas utama dari ALU adalah melakukan perhitungan aritmatika
(matematika) yang terjadi sesuai dengan instruksi program. Rangkaian
pada ALU (Arithmetic and Logic Unit) yang digunakan untuk menjumlahkan
bilangan dinamakan dengan Adder. Adder digunakan untuk memproses operasi
aritmetika, Adder juga disebut rangkaian kombinasional aritmatika.
Ada 3 jenis adder:
1. Rangkaian Adder dengan menjumlahkan dua bit disebut Half Adder.
2. Rangkaian Adder dengan menjumlahkan tiga bit disebut Full Adder.
3. Rangkain Adder dengan menjumlahkan banyak bit disebut Paralel Adder
1. HALF ADDER
Rangkaian Half
Adder merupakan dasar penjumlahan bilangan Biner yang terdiri dari satu
bit, oleh karena itu dinamai Penjumlah Tak Lengkap.
a. jika A = 0 dan B = 0 dijumlahkan, hasilnya S ( Sum ) = 0.
b. jika A = 0 dan B = 1 dijumlahkan, hasilnya S ( Sum ) = 1.
c. jika A = 1 dan B = 1 dijumlahkan, hasilnya S ( Sum ) = 0
jika A = 1 dan B =1 dijumlahkan, hasilnya S ( Sum ) = 0. dengan nilai pindahan cy(Carry Out) = 1
2. FULL ADDER
Sebuah Full
Adder menjumlahkan dua bilangan yang telah dikonversikan menjadi
bilangan-bilangan biner. Masing-masing bit pada posisi yang sama saling
dijumlahkan. Full Adder sebagai penjumlah pada bit-bit selain yang
terendah. Full Adder menjumlahkan dua bit input ditambah dengan
nilai Carry-Out dari penjumlahan bit sebelumnya. Output dari Full Adder
adalah hasil penjumlahan (Sum) dan bit kelebihannya (carry-out).
3. PARALEL ADDER
Rangkaian
Parallel Adder adalah rangkaian penjumlah dari dua bilangan yang telah
dikonversikan ke dalam bentuk binenggap ada dua buah register A dan
B, masing-masing register terdiri dari 4 bit biner : A3A2A1A0 dan
B3B2B1B0.
Rangkaian
Parallel Adder terdiri dari Sebuah Half Adder (HA) pada Least
Significant Bit (LSB) dari masing-masing input dan beberapa Full Adder
pada bit-bit berikutnya. Prinsip kerja dari Parallel Adder adalah
sebagai berikut : penjumlahan dilakukan mulai dari LSB-nya. Jika hasil
penjumlahan adalah bilangan desimal “2” atau lebih, maka bit
kelebihannya disimpan pada Cout, sedangkan bit di bawahnya akan
dikeluarkan pada Σ. Begitu seterusnya menuju ke Most Significant
Bit (MSB)nya.Integer Representation
Apa itu 8 bit, 16 bit, 32 bit, 64 bit?
Bit adalah suatu data yang hanya menyimpan bilangan 0 (false) atau 1 (true).
Sesimpel itu, tapi jika digabung2 akan lebih banyak maknanya
Bit adalah suatu data yang hanya menyimpan bilangan 0 (false) atau 1 (true).
Sesimpel itu, tapi jika digabung2 akan lebih banyak maknanya
Satu byte adalah 8 bit.
Integer yang biasanya ditemukan dalam dunia programming itu biasanya bisa dibedakan jadi 2 tipe, signed dan unsigned.
Apa artinya? Secara sederhana signed itu bisa mengandung nilai negatif, sedangkan unsigned hanya nilai positif.
Integer yang biasanya ditemukan dalam dunia programming itu biasanya bisa dibedakan jadi 2 tipe, signed dan unsigned.
Apa artinya? Secara sederhana signed itu bisa mengandung nilai negatif, sedangkan unsigned hanya nilai positif.
Penjelasan Unsigned Integer
Misalkan 8 bit unsigned integer, yang biasanya disebut char, itu ada integer dengan 8 bit misalnya 01010110.
Angkanya secara sederhana dengan mengubah itu dari basis 2 ke basis 10 (supaya bisa dimengerti manusia
Cara ngubahnya itu tiap posisi bit itu kita kasih nomor dari paling kanan itu 1, semakin ke kiri itu adalah 2 kali dari sebelah kanannya.
Contoh:
Nah yang ada 1 nya itu ditambah semua, kalau contoh di atas 64 + 16 + 4 + 2 = 86.
Artinya range untuk 8 bit unsigned integer itu dari 00000000 = 0 sampe 11111111 = 255. Jadi sekarang harusnya kamu tahu berapa range untuk 16 bit unsigned integer (short). Hal itu juga berlaku untuk 32 bit (long) dan 64 bit (long long).
Angkanya secara sederhana dengan mengubah itu dari basis 2 ke basis 10 (supaya bisa dimengerti manusia
Cara ngubahnya itu tiap posisi bit itu kita kasih nomor dari paling kanan itu 1, semakin ke kiri itu adalah 2 kali dari sebelah kanannya.
Contoh:
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Nah yang ada 1 nya itu ditambah semua, kalau contoh di atas 64 + 16 + 4 + 2 = 86.
Artinya range untuk 8 bit unsigned integer itu dari 00000000 = 0 sampe 11111111 = 255. Jadi sekarang harusnya kamu tahu berapa range untuk 16 bit unsigned integer (short). Hal itu juga berlaku untuk 32 bit (long) dan 64 bit (long long).
Play video ini untuk penjelasan secara visual
Biasanya program - program komputer kalau bicara signed integer itu dia pake Two's complement.
Karena ada lebih dari satu cara untuk mempresentasikan signed integer.
Bit paling kiri di signed integer itu namanya signed bit, itu yang menandakan itu bilangan negatif atau kalau 0, artinya positif, kalau 1 artinya negatif.
Untuk representasi bilangan positif, sama kayak sebelumnya dengan bit paling kiri itu 0.
Untuk representasi bilangan negatif ini yang agak dikit ribet, jadi caranya semua bit diinvert dulu semuanya (0 jadi 1, 1 jadi 0), dan kita memperoleh angka yang positif, tapi sebelum dibaca, kita harus tambah satu dulu baru kita baca sebagai angka positif.
Contoh bilangan negatif : 11101000
Pertama kita tau itu negatif (ngeliat bit pertama), karena itu kita invert semua bitnya : 00010111
Trus kita tambah 1 ke bilangan itu (penjumlahan basis 2 ya, diinget) :
1
2
3
4
5
| 111 <<< caret00010111 1-------- +00011000 |
Jadi hasilnya 00011000, trus diitung pake kayak ngitung positif, 16 + 8 = 24. Jadi karena kita tahu ini negatif, hasilnya jadi -24.
Dan artinya range untuk 8 bit signed integer itu 1000000 = -128 sampe 01111111 = 127. Dan cara yang sama berlaku untuk 16 bit, 32 bit, dan 64 bit.
Dan kalau ada yang bingung kenapa dirancang kayak gini, jawabannya ada pada penjumlahan dua bilangan, karena kalau pakai kayak gini menjumlahkan positif sama negatif value itu gampang. Seandainya 86 (01010110) dijumlah dengan -24 (11101000), untuk ngejumlahin keduanya tinggal kayak ngejumlahin binary biasa.
1
2
3
4
5
| 11 <<< caret 01010110 11101000--------- +x00111110 |
Bisa dilihat pas ngejumlahin bisa lebih dari 8 bit, karena itu yang lewat itu dibuang, hasilnya cuman ngambil 00111110, dan itu adalah 32 + 16 + 8 + 4 + 2= 62 dimana 86 + (-24) = 62.
Nah karena bisa lebih dari 8 bit dan ada bit yang dibuat ini yang biasanya menyebabkan angka gede banget ujung2nya jadi negatif, misalnya kita punya 127 dalam 8 bit signed integer, kita tambahin satu aja, dia bakal menjadi -128 (muter lagi).
Integer Arithmetic
1. Pengertian Bilangan Bulat
Bilangan bulat terdiri dari
– bilangan asli : 1, 2, 3, …
– bilangan nol : 0
– bilangan negatif : …, -3, -2, -1
Bilangan Bulat dinotasikan dengan : B = {…, -3, -2, -1, 0, 1, 2, 3, …}
Bilangan lain yang berada dalam bilangan bulat, di antaranya adalah bilangan:
a. Cacah : C = {0, 1, 2, 3, 4, …}
b. Ganjil : J = {1, 3, 5, 7, …}
c. Genap : G = {2, 4, 6, 8, …}
d. Cacah Kuadrat : K = {0, 1, 4, 9, …}
e. Prima : {2, 3, 5, 7, 11, …}
– bilangan asli : 1, 2, 3, …
– bilangan nol : 0
– bilangan negatif : …, -3, -2, -1
Bilangan Bulat dinotasikan dengan : B = {…, -3, -2, -1, 0, 1, 2, 3, …}
Bilangan lain yang berada dalam bilangan bulat, di antaranya adalah bilangan:
a. Cacah : C = {0, 1, 2, 3, 4, …}
b. Ganjil : J = {1, 3, 5, 7, …}
c. Genap : G = {2, 4, 6, 8, …}
d. Cacah Kuadrat : K = {0, 1, 4, 9, …}
e. Prima : {2, 3, 5, 7, 11, …}
2. Membandingkan Bilangan Bulat
Dengan memperhatikan tempat pada garis bilangan, dapat kita nyatakan (dalam contoh) bahwa :
a. 7 > 4, karena 7 terletak di sebelah kanan 4,
b. (-5) < 2, karena (-5) terletak di sebelah kiri 2, dan lain sebagainya.
Dengan memperhatikan tempat pada garis bilangan, dapat kita nyatakan (dalam contoh) bahwa :
a. 7 > 4, karena 7 terletak di sebelah kanan 4,
b. (-5) < 2, karena (-5) terletak di sebelah kiri 2, dan lain sebagainya.
3. Penjumlahan dan Sifatnya
Salah satu Rumus penting :
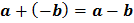
Contoh : 7 + (-10) = 7 – 10 = -3
Sifat-sifatnya :
a. Komutatif :
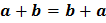
b. Asosiatif :
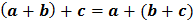
c. Tertutup :
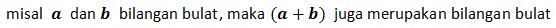
d. Memiliki identitas :

e. Invers penjumlahan :
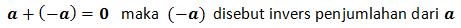
Salah satu Rumus penting :
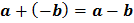
Contoh : 7 + (-10) = 7 – 10 = -3
Sifat-sifatnya :
a. Komutatif :
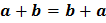
b. Asosiatif :
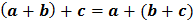
c. Tertutup :
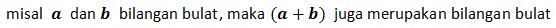
d. Memiliki identitas :

e. Invers penjumlahan :
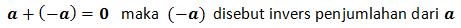
4. Pengurangan
Pengurangan merupakan lawan (invers) dari penjumlahan.
Rumus :
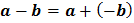
Contoh : 8 – (-2) = 8 + 2 = 10
Pengurangan merupakan lawan (invers) dari penjumlahan.
Rumus :
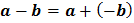
Contoh : 8 – (-2) = 8 + 2 = 10
5. Perkalian dan Sifatnya
contoh :
3 x (-2) = (-2) + (-2) + (-2)

Sifat-sifat :

contoh :
3 x (-2) = (-2) + (-2) + (-2)

Sifat-sifat :

6. Pembagian
Pembagian adalah kebalikan (invers) dari perkalian.
Rumus :
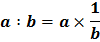
Pembagian adalah kebalikan (invers) dari perkalian.
Rumus :
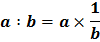
7. Perpangkatan dan Sifat


8. Akar Pangkat Dua dan Akar Pangkat Tiga

Floating Point Representation
Floating-point atau bilangan titik mengambang, adalah sebuah format bilangan yang dapat digunakan untuk merepresentasikan sebuah nilai yang sangat besar atau sangat kecil. Bilangan ini direpresentasikan menjadi dua bagian, yakni bagian mantisa dan bagian eksponen (E). Bagian mantisa menentukan digit dalam angka tersebut, sementara eksponen menentukan nilai berapa besar pangkat pada bagian mantisa tersebut (pada posisi titik desimal). Sebagai contoh, bilangan 314600000 dan bilangan 0.0000451 dapat direpresentasikan dalam bentuk bilangan floating point: 3146E5 dan 451E-7 (artinya 3146 * 10 pangkat 5, dan 451 * 10 pangkat -7).
Kebanyakan CPU atau mikroprosesor sederhana tidak mendukung secara langsung operasi terhadap bilangan floating-point ini, karena aslinya mikroprosesor ini hanya memiliki unit aritmetika dan logika, serta unit kontrol yang beroperasi berdasarkan pada bilangan bulat (integer) saja.
Perhitungan atau kalkulasi terhadap nilai floating point pada jenis mikroprosesor sederhana dapat dilakukan dengan menggunakan perangkat lunak, sehingga operasinya sangat lambat. Untuk itulah, sebuah prosesor tambahan dibutuhkan untuk melakukan operasi terhadap jenis bilangan ini, yang disebut dengan unit titik mengambang.
Dalam bahasa pemrograman, khususnya keluarga bahasa pemrograman C, bilangan titik mengambang direpresentasikan dengan tipe data float.
Bilangan Floating-Point 32-bit (single-precision)
Bilangan floating-point 32-bit tersusun atas (Gambar 0.1↓):
- 1 bit tanda (S),
- 8 bit eksponen (E), dan
- 23 bit untuk mantisa (M)
Field eksponen adalah radix 2. Nilai eksponen bisa negatif atau positif untuk menyatakan bilangan yang sangat kecil atau sangat besar. Format eksponen yang digunakan adalah excess-127. Nilai 127 ditambahkan dari nilai eksponen sebenarnya (Exp), yaitu Exp = E − 127. Dengan excess-127, nilai E akan selalu positif dengan jangkauan 0 sampai 255.
- Nilai ekstrem adalah untuk E=0 dan E=255
- E=0 menyatakan bilangan NOL (jika M = 0) dan subnormal (jika M ≠ 0)
- E=255 menyatakan bilangan TAK TERHINGGA (jika M = 0) dan NAN/not-a-number (jika M ≠ 0);
- Nilai normal adalah 1 ≤ E ≤ 254 yang menunjukkan nilai eksponen sebenarnya dari -126 sampai 127
- Contoh: Emin(1) = − 126, E(50) = − 77 dan Emax(254) = 127;
| Eksponen (E) | Mantissa=0 | Mantissa ≠ 0 | Persamaan |
| 0 | 0, -0 | subnormal | ( − 1)S × 0.bit signifikan × 2 − 126 |
| 1-254 | Nilai ternormalisasi | ( − 1)S × 1.bit signifikan × 2E − 127 | |
| 255 | ∞ | bukan bilangan (NAN=not-a-number) | |
Table 0.1 Nilai eksponen di format floating-point 32-bit
Saat nilai mantisa (M) dinormalisasi, most significant bit (MSB) selalu 1. Namun, bit MSB ini tidak perlu disertakan secara eksplisit di field mantisa (Tabel 0.1↑). Nilai mantisa yang sebenarnya adalah1.M, sehingga nilai bilangan floating-pointnya menjadi:
Di bilangan subnormal, nilai mantisa sebenarnya adalah 0.M, sehingga bilangan floating-pointnya menjadi:
Dengan mantissa 23 bit ini ditambah 1 bit implisit, total presisi dari representasi floating-point 32-bit ini adalah 24 bit atau sekitar 7 digit desimal (yaitu 24 × log10(2) = 7.225).
Dalam pemrograman, suatu bilangan single-precision ini dideklarasikan dengan tipe data float(bahasa C, C++, Java) dan single (Pascal, VB, MATLAB).
float anumber; // 32-bit single precision numberint main(){anumber = -1.1245;...return 0;}
Contoh 1
Bilangan floating-point dinyatakan dengan B = 0x3E600000 . Nyatakan B sebagai bilangan pecahan desimal.
Representasi bilangan floating-point 32-bit dapat dinyatakan seperti Gambar 0.2↓.
Jadi, B = 0x3E6300000 menyatakan bilangan floating-point 0.21875
Figure 0.2 Contoh bilangan floating-point 32-bit B = 0x3E60000
Bilangan Floating-Point 64-bit (double-precision)
Bilangan floating-point 64-bit tersusun atas (Gambar 0.6↓):
- 1 bit tanda (S),
- 11 bit eksponen (E), dan
- 52 bit untuk mantisa (M)
Seperti halnya dengan bilangan single-precission, bit tanda (S) menyatakan bilangan positif jika S=0 dan negatif jika S=1. Field eksponen adalah radix 2. Nilai eksponen bisa negatif atau positif untuk menyatakan bilangan yang sangat kecil atau sangat besar. Format eksponen yang digunakan adalah excess-1023. Nilai 1023 ditambahkan dari nilai eksponen sebenarnya (Exp), yaitu Exp = E − 1023. Dengan excess-1023, nilai E akan selalu positif dengan jangkauan 0 sampai 2047.
- Nilai ekstrem adalah untuk E = 0 dan E = 2047
- E=0 menyatakan bilangan NOL (jika M = 0) dan subnormal (jika M ≠ 0)
- E=2047 menyatakan bilangan TAK TERHINGGA (jika M = 0) dan NAN/not-a-number (jika M≠ 0) (Tabel 0.2↓);
- Nilai normal adalah 1 ≤ E ≤ 2046 yang menunjukkan nilai eksponen sebenarnya dari -1022 sampai 1023
- Contoh: Emin(1) = − 1022, E(100) = − 923 dan Emax(2046) = 1023;
| Eksponen (E) | Mantissa=0 | Mantissa ≠ 0 | Persamaan |
| 0 | 0, -0 | subnormal | ( − 1)S × 0.bit signifikan × 2 − 1022 |
| 1-2046 | Nilai ternormalisasi | ( − 1)S × 1.bit signifikan × 2E − 1023 | |
| 2047 | ∞ | bukan bilangan (NAN=not-a-number) | |
Table 0.2 Nilai eksponen di format floating-point 64-bit
Nilai mantisa (M) dinormalisasi, yang berarti most significant bit (MSB) selalu 1. Bit MSB ini tidak perlu disertakan secara eksplisit di field mantisa. Nilai mantisa sebenarnya adalah 1.M, sehingga nilai bilangan floating-pointnya menjadi:
Dengan mantissa 52 bit ini ditambah 1 bit implisit, total presisi dari representasi floating-point 32-bit ini adalah 53 bit atau sekitar 16 digit desimal (yaitu 53 × log10(2) = 15.995).
Dalam pemrograman, suatu bilangan single-precision ini dideklarasikan dengan tipe data double(bahasa C, C++, Java).
double anumber; // 64-bit double precision numberint main(){anumber = -1.1245;...return 0;}
Contoh 5
Bilangan floating-point dinyatakan dengan B = 0x3FD5000000000000 . Nyatakan B sebagai bilangan pecahan desimal.
Representasi bilangan floating-point 64-bit dapat dinyatakan seperti Gambar 0.7↓.
Jadi, B = 0x3FD5000000000000 menyatakan bilangan floating-point 0.328125
Figure 0.7 Contoh bilangan floating-point 64-bit B = 0x3FD5000000000000 = 0.328125
Floating Point Arithmetic
Sistem penempatan titik desimal dengan cara membagi word menjadi dua bagian. Satu bagian berisi angka pecahan, sebagian lainnya merupakan eksponen dari sepuluh. Posisi efektif dari titik desimal akan berubah ketika eksponennya diubah. Sistem ini digunakan untuk menyatakan hasil perhitungan yang sangat besar atau sangat kecil.
Sumber terkait :
1. http://lookupmens.blogspot.com/2011/03/pengertian-dan-cara-kerja-arithmatic.html
2. http://id.wikipedia.org/wiki/Berkas:ALU_symbol.svg
3. http://teknikrandi.wordpress.com/2013/10/21/2/
4. http://alijayameilio.blogspot.com/2013/07/quick-integer-representation.html
5. http://id.wikipedia.org/wiki/Floating-point
6. http://didik.blog.undip.ac.id/2012/06/01/bilangan-floating-point/
Visit my another blog!
aliamutiamayanda.wordpress.com












No comments:
Post a Comment